28.6.2024
Alex Karrila har tillsammans med Fieldsmedaljören Hugo Duminil-Copin genom sexnodersmodellen med hjälp av axiom lyckats bevisa resultat som hittills endast varit möjligt att bevisa med fysiska experiment.
Som tonåring tränade Alex Karrila tävlingsmatematik. Han hade talang men märkte att han inte kunde ge upp tänkandet på de hemuppgifter som hörde till, och han slutade delta.
– Alla jag känner som blivit matte- eller fysikproffs har visat intresse och begåvning redan i skolåldern. Därtill krävs det mycket jobb och att man besitter egenskaper som tålamod och uthållighet. Att jag fortsatte tänka på hemuppgifterna, vilket gjorde att jag slutade med tävlandet, var kanske också den egenskap som gjorde att jag till slut blev matematiker, säger Karrila.
Som ung tänkte Karrila att han skulle bli fysiker eller ingenjör. Intresset för fysik gjorde att han studerade teknisk fysik på Tekniska högskolan i Otnäs i ett och ett halvt år innan han insåg att han inte är fysiker.
– Jag är i och för sig fortfarande matematisk fysiker, men med betoning på matematik.

– Karikerat kan man beskriva skillnaden mellan matematik och fysik så att man i fysiken vill komma snabbt framåt i lösandet av riktiga, komplicerade problem. Formaliteten i argumenten kan variera från teori till numerik och simulation, till konceptuella argument, eller helt enkelt till experimentella observationer. Det är inte så mycket frågan om matematiskt vattentät logik, transparent framställning, eller att syna eller reducera axiomen man grundar sin problemlösning på.
– Matematiken utgår igen från axiom; sådant man medger att man antar, och sedan försöker man komma till sina slutsatser med glasklara och oemotsägliga motiveringar och samtidigt reducera antalet axiom och antaganden.
– Jag är förmodligen besatt av detaljer, men det som tilltalar mig inom matematiken är att i välskriven matematik finns det inga tvivel.
Nya insikter i tvådimensionell statistisk fysik
Vid Åbo Akademi fungerar Alex Karrila som biträdande professor och Finlands Akademiforskardoktor vid ämnet matematik. I en nyligen publicerad artikel bevisar Karrila med medförfattare, att sexnodersmodellen, som är en arketypisk slumpfältsmodell inom tvådimensionell statistisk fysik, befinner sig i en fluktuerande fysikalisk fas. Eller matematiskt uttryckt: sexnodersmodellen visar tecken på att vara en analog i fältform av den välkända Gausskurvan.
En av medförfattarna, och Karrilas tidigare postdoc-handledare, Hugo Duminil-Copin, tilldelades år 2022 Fieldsmedaljen för ”lösningen av bestående problem i sannolikhetsteorin om fastransitioner i statistisk fysik, i synnerhet i tre och fyra dimensioner”.
Den tredimensionella världen är ännu lite för komplicerad för oss detaljbesatta, men nu förstår vi aningen bättre statistisk fysik i två dimensioner
Fieldsmedaljens betydelse inom matematiken jämförs ofta med den betydelse Nobelpriset har inom andra vetenskaper.
– Duminil-Copin är väldigt driftig och ambitiös, men samtidigt är han ändå jordnära och har ett sinne för humor, han har också en massa samarbetspartners. Även i jämförelse
med andra toppmatematiker är hans intuition och insyn, för att inte tala om hans litteraturkännedom, häpnadsväckande.
– Man kunde sammanfatta det så att han är en specialindivid som vuxit upp och trivts på den franska scenen där matematik, sannolikhetslära och forskning i allmänhet uppskattas och finansieras stort.
Från leksaksmodeller till Brownska rörelser
Det som Karrila oftast jobbar med grundar sig på slumpmodeller och befinner sig i skärningspunkten mellan matematisk statistisk fysik och sannolikhetslära.
– De slumpmodeller vi matematiker studerar är oftast är en kraftigt förenklad abstraktion av den problematik som den representerar. Sådana modeller kallas, med rätta, ”leksaksmodeller”. Men trots reduktionen fungerar leksaksmodellerna ofta på den problemlösning de är kalibrerade mot.
– Ett exempel på något ur den fysiska världen som går att slumpmodellera är partiklar i luften som tecknar slumpmässiga banor, så kallade värmerörelser.
Grovt talat är energin förknippad till värmerörelsen – det som vi observerar som temperatur. En stor matematisk framgång under 1900-talet var introduktion av den Brownska rörelsen; den matematiska värmerörelsen.
– Man kan faktiskt observera Browns rörelse om man med mikroskop tittar på till exempel växtplanktion eller pollenpartiklar i vatten – de brukar ”rymma ur siktet”. Ett följdfenomen som man ser med blotta ögat, som spelar en viss roll i diverse tillämpningar, och som förklaras både konceptuellt och matematiskt av den Brownska modellen, är diffusionen, det vill säga blandningen av partikelkoncentrationer med värmerörelse. Det fenomenet kan vi iaktta om vi till exempel försiktigt pipetterar en droppe vattenfärg i ett glas fyllt med rent vatten: med värmerörelsen av färgämnespartiklarna sprids och utspäds så småningom det färgade området i glaset, tills allt är jämnt pastellfärgat.
– Som kuriosa kan nämnas att om man är mindre försiktig med pipetteringen så ser man en kombination av strömning och diffusion. Det är ett fenomen som kräver både strömningsmekanik och den Brownska diffusionsmodellen om man vill förklara det matematiskt.
Diskretiserad geometri
– De modeller jag studerar lever ofta i en ”diskretiserad geometri”, säger Karrila.
I motstats till den vardagliga betydelsen av ”finkänslig” eller ”subtil” innebär diskret inom matematiken, fritt översatt från engelskan på bakpärmen till matematikern N.L. Biggs bok Discrete Mathematics, ”matematik som handlar om strukturer skapade ur ett ändligt antal beståndsdelar, snarare än koninuerliga strukturer”.
–Ovanstående är ingen formell matematisk definition, men nog ett begrepp som alla matematiker känner till, eller åtminstone känner igen. Låt oss som inledande exempel tänka på hur elektroner rör sig i dopade halvledningsmaterial.
Halvledningsmaterial, till exempel kisel, är ämnen som leder elektricitet under specifika omständigheter och vars atomer binds till varandra i en kristall-, eller gitterstruktur. Dopade halvledare är halvledare som fått material tillsatta som har en elektron ”för mycket”, eller en elektron ”för lite” kring sina atomer, vilket leder till att atomerna fortfarande ligger i ett gitter, där de övriga elektronerna rör på sig och förbättrar materialets ledningsegenskaper Låt oss studera värmerörelsen hos en elektron i frånvaron av ett externt elektriskt fält.
Om det enda vi bevarar är informationen om vilken atom elektronen för tillfället är bunden till, blir rummet ”pixlat”, eller på matematisk jargong: ”diskretiserat”. Det mest sannolika är att elektronen hoppar till närmaste grannatom, eftersom det krävs mycket energi att hoppa någon annanstans, så vi gör det antagandet.
– En sådan här diskret värmerörelse på gitter är fundamentalt annorlunda än den som vi ser hos partiklar som rör sig fritt i vätskor och gaser, såsom vattenfärgsexemplet: elektronens rörelse i halvledaren är bunden till gitterstrukturen. En grov tolkning av ett känt matematiskt resultat av Monroe Donsker från 1951 är dock att en sådan bunden slumprörelse beter sig på samma sätt som en fri rörelse, på längdskalor som är stora i jämförelse med kristallstrukturen.
– I synnerhet gäller även vidare egenskaper av den Brownska rörelsen för den bundna slumprörelsen, som den matematiska beskrivningen av diffusionen av ett stort antal partiklar.
– Den här tidiga matematiska framgångshistorien är ett typexempel på det som jag vill göra: Jag börjar från en modell som naturen dikterar är diskret och studerar objekt såsom slumpgeometri, slumpfält, och korrelationsfunktioner. Förhoppningen är sedan att kunna bevisa att de på längre skalor liknar bättre kända ”icke-diskreta” sannolikhetsmodeller och att dra vidare slutsatser från analysen av dessa kända modeller.
Gibbska slumpfält och fastransitioner
– Exemplet med bunden och fri värmerörelse är en klassiker, men det saknar två aspekter som är centrala i vårt nya resultat: Gibbsiska slumpfält och fastransition.
– Förresten är det naturligt att rörelsemodellen saknar fastransition, för fysiken håller med om att värmerörelse alltid finns ovanför den absoluta nollpunkten.
– Mitt nästa, nästan vardagliga exempel är Curietemperaturen av ferromagnetiska ämnen, och dess förklaring med Lenz-Ising-modellen, först studerad av Wilhem Lenz student Ernst Ising på 1920-talet.
Ferromagnetism innebär att vissa ämnen, som järn eller kobolt, blir starkt magnetiserade av, och således förstärker, ett externt magnetfält. Reaktionen på externa magnetfält hos ämnen som inte är ferromagnetiska kan knappt observeras. Fransmannen Pierre Curie upptäckte år 1895 att om ferromagnetiska ämnen värms till en tillräckligt hög temperatur förlorar de sina särskilda magnetiska egenskaper och börjar bete sig som ”vanliga ämnen”. En fastransition sker alltså i det magnetiska beteendet vid en viss temperatur och det syns alltså i att ämnet förlorar de magnetiska egenskaper det hade på lägre temperaturer. Temperaturen där det här sker kallas ämnets Curietemperatur och för exempelvis järn är Curietemperaturen cirka 770 Celsiusgrader.
– Det betyder att glödhett järn inte fastnar i en magnet, och det är ett experiment som man kan göra i ett vanligt högstadiums fysiklabb – men tyvärr inte här i matematikens kontorsutrymmen!
Den som är intresserad av experimentet, men som av till exempel brandsäkerhetsskäl inte bör eller får leka med eld och mycket höga temperaturer hemma, kan söka upp videoklipp på nätet med nyckelorden ”Curie temperature”.
– Isings modell för ferromagnetism var att järnet består av mikroskopiska magneter, låt oss säga i formen av kubiska ”pixlar”, och varje mikromagnet pekar antingen nord- eller sydvart. Magnetiseringen är alltså ett fält som tar ett av två möjliga värden på var pixel. Dessa mikromagneter växelverkar sedan med sina närmaste grannpixlar och med en eventuell extern magnet, så att de helst vill peka åt samma håll. Det vill säga; detta tillstånd har lägre potentialenergi. I detta skede låter det självklart att järnet magnetiseras, men mikromagneterna kan, grovt sagt, få små slumpmässiga energistötar av värmerörelser och magnetiseras ”åt fel håll”.
– Modellen utgår från en Gibbsfördelning som alltid är en dragkamp mellan entropi och energi.
En ”fördelning” betyder en matematisk beskrivning av ett slumpsystem. Gibbsfördelningen (eller Boltzman-Gibbs-fördelningen) är en allmän termodynamisk princip om hur sannolikheten ett visst tillstånd av systemet, i detta fall vissa magnetiseringar för varje mikromagnet, bestäms utifrån temperaturen och tillståndets potentialenergi.
– Energiminimitillståndet är i alla temperaturer det mest sannolika enskilda tillståndet, men ju högre temperatur, desto mer sannolikhet får även de mer högenergiska tillstånden. Den nämnda dragkampen mellan entropi och energi uppstår när antalet olika tillstånd, grovt sagt; entropin, förespråkar utfallet av ett högenergiskt tillstånd, medan Gibbs sannolikheter förespråkar ett lågenergiskt tillstånd. I en sådan modell förekommer ofta en fastransition när man ökar temperaturen; högenergetiska tillstånd blir vid en viss punkt mer frekventa.
– Och det är just en sådan fastransition som vi ser med Isings modell. Den är ju en överförenkling och modellen innehåller okända parametrar, så den förutspår till exempel inte fastransitionstemperaturen, men det kvalitativt rätta beteendet bekräftar Lenz och Isings intuition om ferromagnetismens ursprung.
Sexnodersmodellen
Sexnodersmodellen, som den nyligen publicerade artikeln där Karrila medverkade handlade om, introducerades ursprungligen av den svensk-amerikanske kemisten Linus Pauling i ett försök att modellera isens gitterstruktur. Strukturen är slumpmässig men äger vissa naturliga regler som imiterar vätebindningarna vattenmolekylerna emellan.
– I och med att vi, och många andra före oss, studerar den i två dimensioner skall den betraktas som en leksaksmodell. Fullt matematiska studier av tredimensionella modeller inom statistisk mekanik är ökänt svåra, och det gav, som sagt, till slut Duminil Copin Fieldsmedaljen.
– En Paulings konfiguration av ismolekyler kan avbildas till en så kallad höjdfunktion och vice versa. Matematiskt kan vi alltså lika väl betrakta vilketdera objektet som helst, och avbilda det till det andra. En alternativ tolkning av modellen är då att det motsvarande höjdfältet är som en trumhinna, som får en aning energi av värmefluktuationer enligt Gibbs lag och ligger därför inte alldeles platt.
– Det har sedan tidigare varit känt att en sådan trumhinna ändå ligger väsentligen
platt i låga temperaturer. Vi analyserade det okända temperatursintervallet och lyckades bevisa att hinnan har stora höjdfluktutationer – alltså sker det en fastransition från ordning till kaos, som är analog till den som man ser i Isings ferromagneter.
– Om man vill tolka det genom vattenisen så ska begreppet temperatur snarare ersättas med potentialenergi: om energiskillnaden mellan en ”naturlig” och ”böjd” geometri av en vattenmolekyl är stor så är en överväldigande massa av vattenmolekylerna i den naturliga geometrin i vattenisen; om den är liten så är isens mikrostruktur kaotisk.
– För fysiker torde saken ha varit klar sedan Elliot Liebs resultat från 1967. Kravnivån på vad som betraktas som bevis i matematiken är så mycket högre att vi kommer 57 år efter. Eller så är vi matematiker kanske lite trögtänkta. Betydelsen av den här leksaksmodellen på tvådimensionell is hänger ihop med att den inom sannolikhetsteorin kan kopplas till många andra viktiga slumpmodeller.
– Förenklat betyder en koppling att man med en slumpgenerator kan simulera en sexnoders-modell och sedan avbilda den, helt utan, eller med bara lite slumpgenerering, till en annan modell. Den är alltså mer komplicerad än, men samtidigt lik, många tidigare undersökta modeller. Å ena sidan kan sexnodersmodellen slå samman det som man gör med andra modeller, å andra sidan är detta resultat ett tecken på att sex noders modellen är matematiskt hanterbar och likadana resultat kan sökas i den i ännu mer invecklade modeller.
– Den tredimensionella världen är ännu lite för komplicerad för oss detaljbesatta, men nu förstår vi aningen bättre statistisk fysik i två dimensioner.
Resultaten kan även tolkas med hänvisning till statistik snarare än fysik.
– Ett nolldimensionellt rum är en punkt, och en funktion på det rummet är ett enda tal. Den centrala gränsvärdessatsen dikterar att ett slumptal – det vill säga slumpfunktion på det nolldimensionella rummet, som består av summan av många bidragande slumpmässiga faktorer är med mycket allmänna antaganden approximativt normalfördelat.
Det är därför som fördelningen är ”normal”: den förekommer nästan överallt, som till exempel människors längd i ett givet land. Grafiskt representeras normalfördelningen av en Gausskurva.
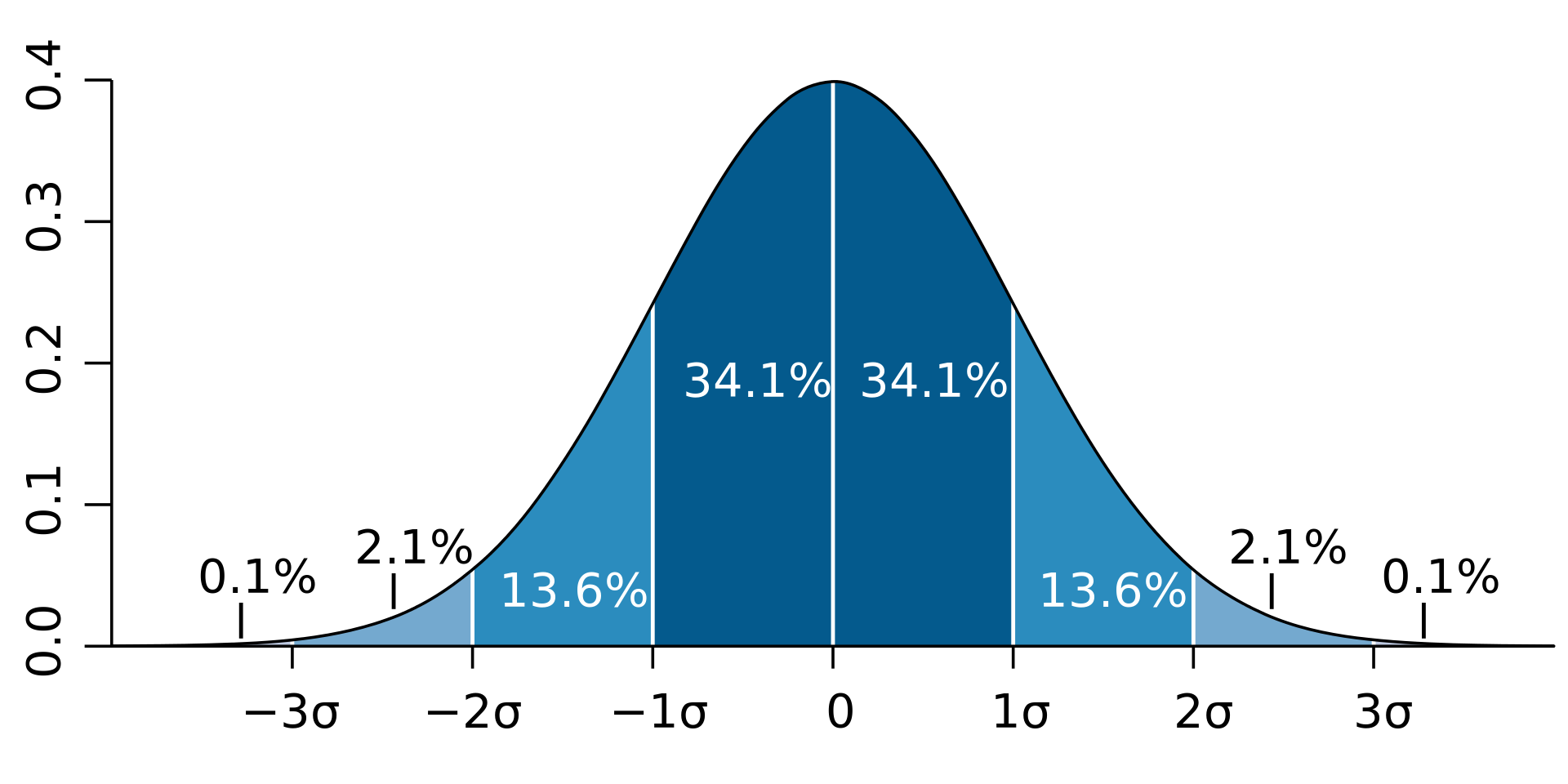
Om man kastar en sex-sidig tärning kommer man att se antingen 1,2,3,4,5 eller 6 med samma 16,7 procents chans varje gång – inget av resultaten är mer sannolikt än något annat. Adderar man några tärningar, säg att man har tre, eller fler tärningar, börjar sannolikheten för att ett visst tal ska dyka upp forma en klockformad sannolikhetskurva (bell curve). Om man som exempel kastar tre sex-sidiga tärningar och räknar ihop resultaten ligger de möjliga resultaten mellan 3 och 18 – men till skillnad från att bara kasta en enkel tärning där varje värde hade samma chans att dyka upp, har man med tre kastade tärningar en fördelning mellan olika sannolikheter. Då har man en 12.5 procents chans att få resultaten 10 eller 11, 11,57 procents chans att få 9 eller 12, och med fallande sannolikhet fram till 3 och 18 som man bara har en 0.46 procents chans att få. Det finns alltså en stabilitet kring medelresultaten medan de yttre resultaten blir mer osannolika ju längre utåt man går. Inom statistik och sannolikhetslära är Gausskurvan ett grundläggande begrepp. På bilden ovan ser man sannolikheten för olika resultat givna inom en normalfördelning, så att de resultaten på båda sidan om mitten har en chans på 34.1 procent var (alltså 68,2 procent av alla resultat kommer att falla inom den snävaste normalfördelningen), medan lite mer än 95 procent av alla resultat finns inom två standardavvikelser och 99,7 procent inom tre standardavvikelser. Figuren gjord av M.W. Toews. Publicerad enligt CC-BY-2.5.
– Ett endimensionellt rum är en linje, ofta säger vi tidslinje, och en funktion på det rummet är en kurva, som vi kan till exempel tänka på som beskrivningen av en rörlig partikels höjd från marken som en funktion av tiden. Det tidigare nämnda teoremet av Donsker dikterar att en rörelse som består av summan av många små slumpmässiga stötar mycket allmänt är approximativt; en Brownsk rörelse. Igen är det därför som många processer, till exempel en partikels eller en aktiekurs rörelse som en funktion av tiden, liknar den Brownska rörelsen.
– Ett tvådimensionellt rum är ett plan, och en funktion på det kan vi tänka på som en beskrivning av markytans höjd på kartpapper, eller snitthöjd per kartpixel om rummet är diskretiserat.
– Men plötsligt finns det, i två, eller fler dimensioner, ingen motsvarighet till de två ovan nämnda välkända resultaten, och det verkar vara formidabelt svårt att bevisa, ens för en given modell och ännu värre för modeller med allmänna antaganden. Vårt resultat är ett steg mot ett sådant resultat för det slumpfält som naturligt kopplas till sexnodersmodellen.
Sexnodersmodellen förklarad för folk som kan simma i den djupare bassängen
Här kommer sex-noders-modellen presenterad av Alex Karrila i större detalj. Den som hänger med, hänger med:
– En tolkning av sex-noders-modellen, även om det inte är frågan om den vanligaste tolkningen, är att det motsvarande höjdfältet är som en trumhinna, som får en aning energi av värmefluktuationer och därför inte ligger alldeles platt. Det tvådimensionella rummet är alltså diskretiserat, det vill säga pixlat, med små kvadrater, och höjden på hinnan får endast anta heltalsvärden 0, 1, -1, 2, -2,… i varje pixel.
– Modellen har dock ingen tidsparameter, det vill säga, vi betraktar tillståndet i ett sådant system vid en fixerad tidpunkt.
Jag är förmodligen besatt av detaljer, men det som tilltalar inom matematiken är att i välskriven matematik finns det inga tvivel
– Därtill har fältet ett paritetsfenomen: ”platt” betyder här egentligen ett schackbrädsmönster av fältvärdena 0 och 1. Det här mönstret syns i simulationerna. Under vissa naturliga symmetriantagen har modellen en enda parameter c som är större eller lika med 1. Den kan tolkas så att c = 1 är oändlig temperatur och c = +∞ är nolltemperaturen i Kelvin, och temperaturaxeln är omvänd och spridd över c ∈ [1, ∞). Det är alltså fråga om en Gibbsfördelning, där tillstånden, det vill säga, varje given höjdkonfiguration har vissa fixade energier och när vi krymper c så blir högenergetiska tillstånd mer och mer sannolika.
– Det var tidigare känt att modellen är ”frusen” för c > 2. Matematiskt och samtidigt visuellt betyder detta att man i simulationerna ser ett överväldigande kluster av fältvärden 0, 1, utgörandes ett schackbrädsmönster, i vilket andra värden förekommer endast som ”sm˚a öar”. (Kolla de mittersta bilderna i boxen för simulationer / Red.)
– Det som jag och medförfattarna bevisade är att modellen är ”fluktuerande” för 1 ≤ c ≤ 2, det vill säga det förekommer inte överväldigande kluster av några två på varandra följande tal (0,1 eller 1,2 eller…). Modellen är förstås mycket mer intressant då, än som frusen.